排序算法之堆排序

Posted on | In |

介绍

分析

基本思想:

  1. 将无需的数据构成堆（即用无序数据生成满足堆定义的完全二叉树）
  2. 利用堆排序（即将上一步生成的堆输出，得到排序后的有序数据）

算法描述:

构成堆

  1. 将无序数据放入完全二叉树的各节点

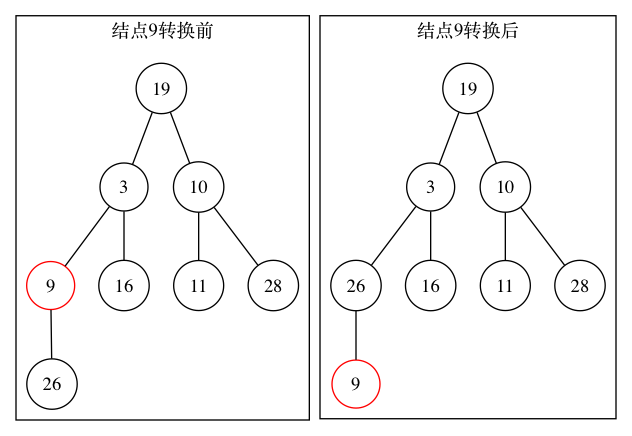
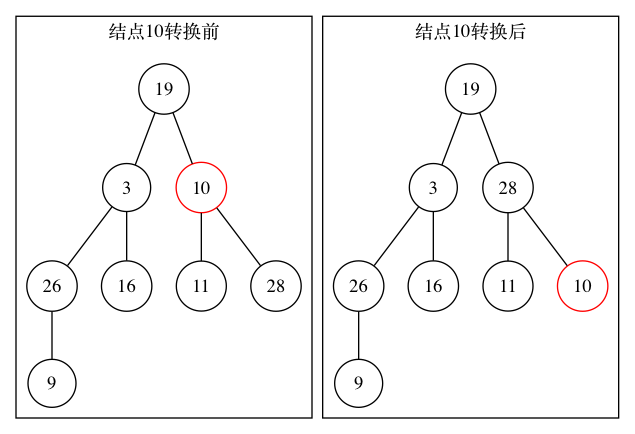
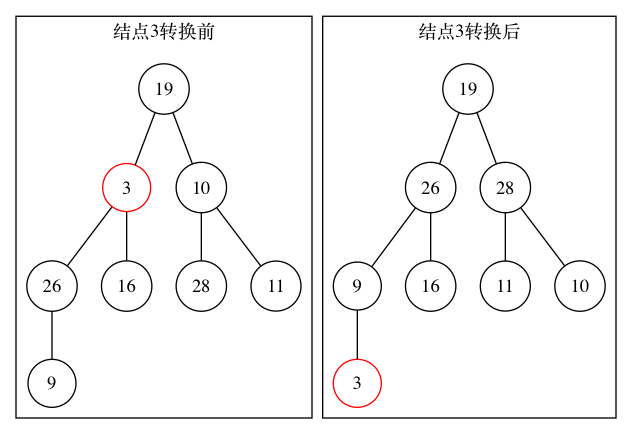
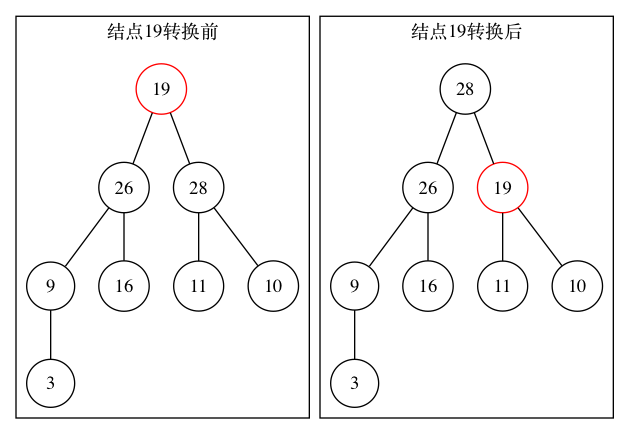
  2. 由二叉树的下层向上层逐层进行父子节点的数据比较，使用一种称为“筛”的运算进行节点数据的调整，直到使节点最后满足堆的条件为止（针对非叶节点）

    2.1 确定Ai的两个子树的最大值，放在Aj中

    2.2 将Ai的数据与Aj的数据进行比较，如果Ai>=Aj,表示Aj为根的子树已构成堆，筛运算完成

    2.3 若Ai<Aj，则将Ai与Aj互换位置，互换位置后可能会破坏以Ai(此时Ai的值为原来的Aj)为根的堆，接着再以Aj为根重复前面的步骤，直到父节点数据大于子节点，或子节点为空时为止

堆排序

  1. 取堆的根节点（最大值），将其放到数组的最后
  2. 重新执行前面介绍的构成堆的方法，最后一个节点排除在外
  3. 重复上面过程，直到只剩下一个节点，即可得到有序的数据

堆排序9结点

堆排序10结点

堆排序3结点

堆排序19结点

C实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
/**
 创建大堆

 @param a 原数组
 @param s 当前结点
 @param n 堆的大小
 */
void HeapAdjus(int a[], int s, int n)
{
    while (2 * s + 1 < n) {
        int j = 2 * s + 1;
        if ((j + 1) < n) {
            //左子树小于右子树，则需要比较右子树
            if (a[j] < a[j + 1]) {
                j++;//序号增加1，指向右子树
            }
        }
        
        //比较s与j为序号的数据
        if (a[s] < a[j]) {
            int t = a[s];
            a[s] = a[j];
            a[j] = t;
            //堆被破坏，需要重新调整
            s = j;
        }
        else {
            //不再需要调整
            break;
        }
    }
}

/**
 堆排序
 
 @param a 原数组
 @param len 数组长度
 */
void heapSort(int a[], int len)
{
    //将a[0]至a[n-1]构成堆
    for (int i = len / 2 - 1; i >= 0; i--) {
        HeapAdjus(a, i, len);
    }
    
    //取根节点与末节点交换
    for (int i = len - 1; i > 0; i--) {
        int t = a[0];
        a[0] = a[i];//与第i个记录交换
        a[i] = t;
        //将a[0]至a[i]重新调整为堆
        HeapAdjus(a, 0, i);
    }
}

/**
 测试堆排序
 */
void testHeapSort()
{
    int arr[8] = { 19, 3, 10, 9, 16, 11, 28, 26 };
    int len = sizeof(arr)/ sizeof(arr[0]);
    
    printf("堆排序前:");
    for (int i = 0; i < len; i++) {
        printf("%d ",arr[i]);
    }
    
    heapSort(arr, len);
    
    printf("\n堆排序后:");
    for (int i = 0; i < len; i++) {
        printf("%d ",arr[i]);
    }
    printf("\n");
}
Swift实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class HeapSort {
    
    
    /// 创建大堆
    ///
    /// - Parameters:
    ///   - a: 原数组
    ///   - i: 当前结点
    ///   - n: 堆的大小
    func HeapAdjust(a: inout [Int], i: Int, n: Int) {
        var s = i
        while 2 * s + 1 < n {
            var j = 2 * s + 1;
            if ((j + 1) < n) {
                //左子树小于右子树，则需要比较右子树
                if a[j] < a[j + 1] {
                    j += 1;//序号增加1，指向右子树
                }
            }
            
            //比较s与j为序号的数据
            if a[s] < a[j] {
                (a[s], a[j]) = (a[j], a[s])

                //堆被破坏，需要重新调整
                s = j;
            }
            else {
                //不再需要调整
                break;
            }
        }
    }
    
    /// 堆排序
    ///
    /// - Parameters:
    ///   - a: 原数组
    ///   - len: 数组长度
    func heapSort(a: inout [Int], len: Int) {
        //将a[0]至a[n-1]构成堆
        for i in (0...len / 2 - 1).reversed() {
            HeapAdjust(a: &a, i: i, n: len)
        }
        
        //取根节点与末节点交换
        for i in (1...len - 1).reversed() {
            (a[0], a[i]) = (a[i], a[0])
            //将a[0]至a[i]重新调整为堆
            HeapAdjust(a: &a, i: 0, n: i)
        }
    }
    
    /// 测试
    func testHeapSort() {
        var arr = [ 19, 3, 10, 9, 16, 11, 28, 26 ]
        print("堆排序前:\(arr)", separator: " ")
        heapSort(a: &arr, len: arr.count)
        print("堆排序后:\(arr)", separator: " ")
    }
}

总结

时间复杂度:

  • 最差O(nlogn)
  • 最优O(nlogn)
  • 平均O(nlogn)

空间复杂度:

  • O(1)

稳定性:

  • 不稳定